|


| |
L'informazione musicale viene rappresentata
in due modi:
La rappresentazione audio codifica il suono
attraverso il sistema tradizionale di notazione musicale.
La codifica audio del suono si realizza
convertendo il segnale analogico in segnale digitale, cioè campionando la forma
dell'onda sonora. Ma vediamo cosa significano prima di tutto i termini analogico
e digitale.
Il segnale analogico è quello in cui è
continua la variazione nel tempo. Il segnale digitale è quello in cui la
variazione nel tempo avviene in modo discreto. Facciamo un esempio:
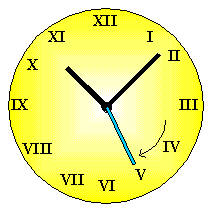
Pensiamo ad un orologio a lancette. Questo
orologio segna le ore, i minuti e i secondi, ma anche i decimi, i
centesimi e così via. Anche se è difficile per l'occhio distinguere i vari
istanti, comunque, sappiamo che egli passa, in modo continuo per ogni istante di
tempo. Se guardiamo un orologio digitale esso segnerà le ore, i minuti e i
secondi, facendo scattare questi ultimi uno ad uno: dalle 10:10:01 alle 10:10:02
l'orologio segnerà sempre le 10:10:01. L'orologio a lancette è un dispositivo
analogico, mentre l'altro, siccome fornisce solo misurazioni discrete, ma non
continue, è detto digitale.
Fig. 1:
Che cosa significa il termine campionare un
segnale?
Campionare significa trovare una
rappresentazione numerica discreta per qualcosa che in origine ha variazione
continua.
Es. Per modificare una registrazione di una
voce fatta con un registratore digitale si potrà utilizzare un computer in grado
di analizzare i dati numerici discreti e quindi modificarli.
L'operazione del campionamento si basa su due
fattori:
La frequenza di campionamento incide sulla
frequenza massima rappresentabile dal segnale digitale.
Il numero di bit incide sul tasso di rumore
aggiunto nella fase di conversione.
Campionamento e tempo (frequenza e teorema
di Niquist)
Il primo problema pratico che si incontra di
fronte alla realizzazione di un campionamento, è di stabilire quante volte in un
certo lasso di tempo vada presa la misurazione del segnale perchè il
campionamento risulti accurato, e quindi il segnale digitale risultante possa
essere riconvertito in segnale analogico senza aver perso le caratteristiche del
segnale originale.
Prendiamo come esempio l'onda sinusoidale.
Fig. 2:
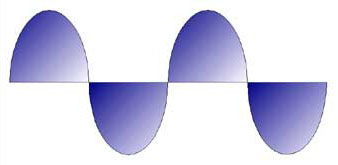
Con un dispositivo prendiamo, in un certo
lasso di tempo, un certo numero di campioni del segnale: ad esempio 14 campioni
per periodo, otterremo una serie di campioni come quelli in figura:
Fig. 3:
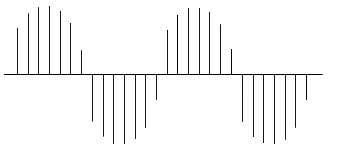
Analizzando la figura notiamo che la
sinusoide originaria è ancora intuibile, per cui possiamo ricostruirla. Ma
immaginiamo di dimezzare la frequenza di campionamento, ossia di raddoppiare il
tempo tra una misurazione e l'altra. Otterremo una serie di campioni meno fitta
della precedente:
Fig 4:
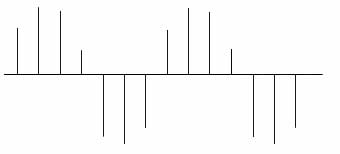
La sinusoide è ancora intuibile, ma è
evidente che abbiamo perso parte dell'informazione originale. Dimezzando ancora,
la situazione diventa quasi critica.
Fig 5:
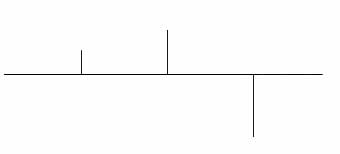
Abbiamo capito dunque che c'è un punto
critico, al di sotto del quale la frequenza di campionamento non può scendere,
pena la perdita totale dell'informazione.
Esiste un importantissimo teorema che ci viene incontro nello
stabilire quale sia questo punto critico, un teorema che si
chiama Teorema di Nyquist - dal nome del suo scopritore -
o anche Teorema fondamentale del campionamento.
Il teorema afferma che:
ogni segnale a banda limitata può essere campionato e
perfettamente ricostruito a patto che la frequenza di
campionamento sia almeno il doppio della frequenza massima
contenuta nella banda del segnale.
Soffermiamoci un attimo: innanzitutto vediamo che la banda del
segnale deve essere limitata: ossia deve esserci una frequenza
massima all'interno del segnale, che non venga mai superata.
Poi, misurata questa frequenza massima, il teorema afferma che
la frequenza del campionamento deve essere almeno doppia di
questa frequenza massima perchè il campionamento possa essere
realizzato con successo.
Ad esempio: se vogliamo campionare il segnale di un basso
elettrico, nel quale la frequenza massima sia, per ipotesi,
300Hz (ovvero l'onda sonora più "veloce" compie 300 cicli al
secondo), la frequenza di campionamento dovrà essere come minimo
di 600Hz, ossia dovranno essere presi almeno 600 campioni in un
secondo.
Se però dobbiamo campionare il segnale di un violino, che
arrivi, ad esempio, fino a 15.000 Hz, sarà necessaria una
frequenza di campionamento di almeno 30.000Hz, ossia si dovranno
prendere almeno 30.000 misurazioni al secondo.
Nella pratica, in ragione del fatto che lo spettro dell'udibile
per l'orecchio umano è compreso tra i 20 e i 20.000Hz, una
frequenza di 40.000Hz dovrebbe essere sufficiente a campionare
ogni possibile suono udibile dall'uomo.
In questa affermazione il condizionale è d'obbligo, perchè nella
pratica intervengono problematiche connaturate alla costruzione
e al funzionamento dei dispositivi, per cui una frequenza
"standard" viene oggi individuata attorno ai 44.100Hz, anche se
sono largamente utilizzate anche frequenze più alte (48.000Hz,
96.000Hz) o, nelle vecchie apparecchiature, più basse (15.000Hz,
30.000Hz).
Campionamento e ampiezza (dinamica, bit e
quantizzazione)
Abbiamo chiarito, brevemente, alcune questioni legate alla
frequenza di campionamento: possiamo dire, in un linguaggio
appena un po' più tecnico, che abbiamo analizzato la questione
nel dominio del tempo - ossia sull'asse orizzontale del grafico
del nostro segnale.
Proviamo a cambiare punto di vista, e analizziamo in generale la
questione dal punto di vista dell'asse verticale: ossia dal
punto di vista dell'ampiezza.
Abbiamo visto che, nel campionamento, andiamo a trasformare in
valori numerici discreti quello che in origine è un segnale
continuo.
Ciò è dovuto al fatto che dobbiamo operare con macchine che
possono gestire solo numeri finiti.
In realtà, chi sa anche solo un po' di informatica, sa che ogni
valore numerico viene conservato in un calcolatore sotto forma
di una sequenza di bit - dove un bit può assumere un valore tra
0 e 1.
Un valore numerico memorizzato nel nostro campionatore dovrà
quindi avere una forma del tipo 0010, o 1011, o 10110101, o
qualcosa di analogo.
Come si applica questa situazione generale al campionamento?
E' evidente che i valori che descrivoro l'ampiezza del segnale
nell'istante in cui avviene il campionamento, dovranno essere
del tipo che abbiamo visto: è chiaro anche, quindi, che essi non
potranno assumere ogni possibile valore numerico (6, 35, 47/17,
pi greco, 4,6666666...), ma potranno in realtà essere scelti in
un insieme ristretto e finito, determinato dal numero di bit che
il calcolatore metterà a disposizione per i valori dell'ampiezza
del segnale.
I numeri dovranno cioè essere approssimati ad uno dei
valori possibili.
E' per questo che, oltre alla frequenza di campionamento,
di un campionatore si dichiara anche la capacità di
quantizzazione.
Quali sono i valori possibili per la quantizzazione?
Prendiamo il caso che il campionatore metta a disposizione 4 bit
per il campionameto. Ciò significa che avremo a disposizione
valori binari da 0000 a 1111, ossia solo 16 "step" di valori
possibili. Questo ci costringerà ad un grafico digitale
piuttosto rozzo, con pochi valori possibili per un segnale che,
invece, possiede moltissime possibilità di variazione dinamica
(pensate a quanti possibili valori di ampiezza può produrre
un'orchestra, dal pianissimo al fortissimo: un direttore
d'orchestra inorridirebbe al pensiero di soli 16 possibili
volumi differenti!).
Già con 8 bit a disposizione la situazione è migliore: il
massimo numero possibile è 11111111, ossia, passando dalla
numerazione binaria a quella in base dieci, 256.
Questo significa che avremo 256 possibili "step" di volume.
In generale, la formula che ci dà il numero di step - o
regioni - di quantizzazione è 2N, dove N è il
numero di bit.
Così ad esempio avremo, con 16 bit (una quantizzazione tuttora
molto in uso), 2N=65.536 regioni, con 24 bit, 2N=16.777.216
regioni.
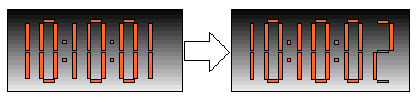
Vediamo ad esempio come cambia la rappresentazione di una
sinusoide, passando da una quantizzazione a 3 bit ad una a 4
bit.
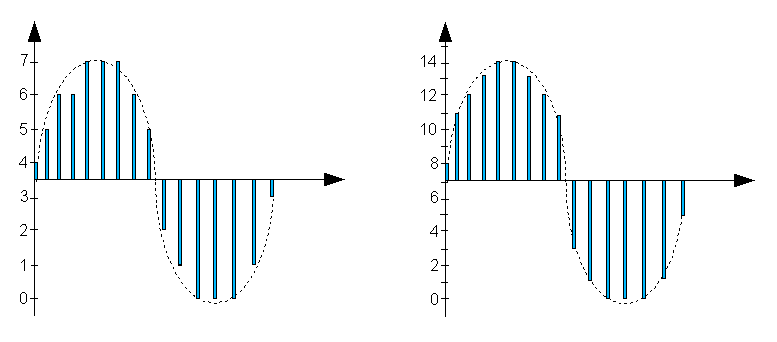
E' facile osservare, da sinistra a destra, che un solo bit di
quantizzazione in più aumenta di molto la precisione del
campionamento.
Ovviamente la piccola panoramica che abbiamo fatto sul
campionamento è solo un'introduzione ad uno studio più
approfondito.
Nei prossimi tutorial sull'argomento vedremo quali sono le
effettive tecniche di campionamento, quali sono i dispositivi
utilizzati, e parleremo di questioni quali aliasing,
sovracampionamento, dither, e così via.
© audiomaster: Michelangelo Izzo |
|
|
.htm_cmp_level010_bnr.gif)
